- Basic Astrodynamics Formulas Pdf
- Basic Astrodynamics Formulas For Beginners
- Basic Astrodynamics Formulas Chart
- Basic Astrodynamics Formulas Free
- The Tsiolkovsky rocket equation, classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity can thereby move due to the conservation of momentum.
- Basic Astrodynamics Formulas Productivity Mac See All. BackgroundClock Entertainment EasyCalculator Utilities Meme Creator Photo & Video Basic Tax Formulas Business Desktop Shades Education Falling Hearts Entertainment More ways to shop: Find an Apple Store.
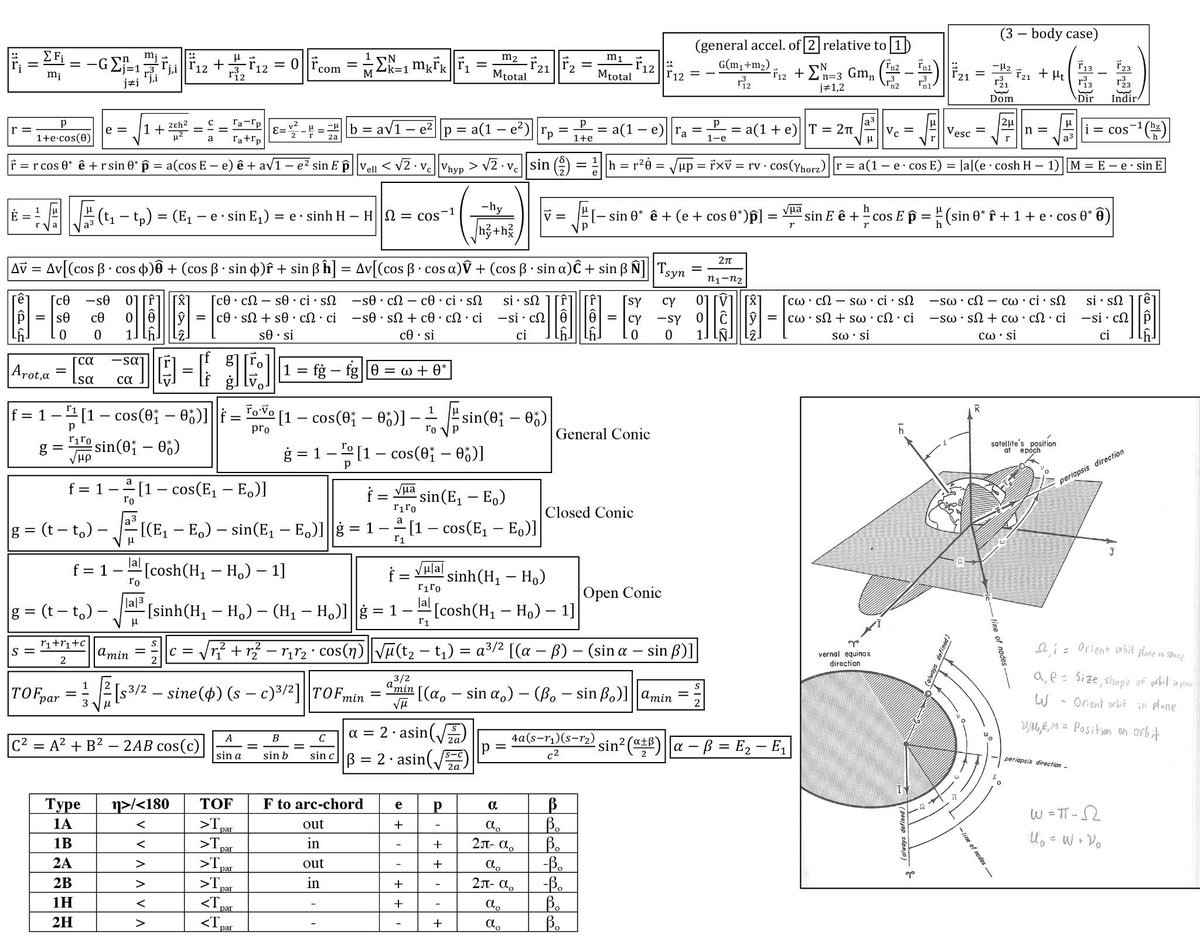
Then, the basic astronomical concepts of reference frames, coordinate systems, orbital elements and time are presented, and various topics which are crucial in modern astrodynamics are addressed.
Postal and E-Mail AddressesAbout the Book
Topics in Astrodynamics builds a mathematical foundation for understanding and analyzing artificial Earth satellite orbits, to includeEarth escape and flyby trajectories. Its chapters first deal with theclassical orbital elements, and then address the fundamental problemof satellite tracking: how to calculate ground traces and look angles, given the orbital elements of an artificial Earth satellite. Element set transformations and Gaussian orbit determination are then treated.
Orbital perturbations are dealt with via the topics of Cowell (numerical) orbit propagation, variation of parameters, and general perturbation theory. The final chapter addresses the fundamental problem of space surveillance: how to calculate an accurate state vector for the orbit of an artificial Earth satellite, given radar or optical observations (or some mix of both), and an initial estimate of the state vector at some epoch.
The book complements currently available works on celestial mechanics ('orbital mechanics applied to celestial bodies') by applying orbital mechanics to the approximately 10,000 artificial Earth satellites whoseorbital elements are to be found in the satellite catalog of NorthAmerican Aerospace Defense Command (NORAD) in Colorado Springs, Colorado U.S.A.
The book's author states, 'Topics in Astrodynamics captures that which is worth passing along from what I myself have learned, worked out, and taught, both as an author and as a user of computer software for orbital analysts, over a space career that has spanned more than three decades.'
Basic Astrodynamics Formulas Pdf
Topics in Astrodynamics was typeset as a 'standard LaTeX book' usingMacKichan Software's Scientific Word; see http://www.mackichan.com. Its 378 pages are sized at 8.5' by 11' and are bound between soft covers by means of a 1-1/8' diameter, 19-ring GBC plastic comb binding. See below for an actual photo of the book and a complete summary of the book's contents.
TOPICS IN ASTRODYNAMICS
Title Page i
Copyright Page ii
Dedication iii
Note on Typeset Manuscript iv
Preface v
Table of Contents ix
List of Figures xvii
Chapter 1. Introduction and Review 1
1.1 Scope 1
1.2 Review of Elementary Mechanics 2
1.2.1 Basic Definitions 2
1.2.2 Newton's Laws of Gravitation 3
1.2.3 Kepler's Laws 5
1.2.4 Work, Energy, and Conservative Forces 5
1.3 Review of the Conic Sections 8
1.3.1 Polar Transformations and Standard Form 8
1.3.2 Conic Sections and Conic Paths 9
1.4 Suggested Reading 12
Chapter 2. The Two-Body Problem 15
2.1 Equations of Relative Motion 15
2.2 Conservation Theorems 17
2.2.1 Conservation of Energy 17
2.2.2 Conservation of Angular Momentum 18
2.3 Solution of the Relative Equations 19
2.3.1 Proof of Kepler's First Law 21
2.3.2 Proof of Kepler's Second Law 25
2.3.3 Proof of Kepler's Third Law 26
2.4 The Flight Path Angle 28
2.5 Position in the Orbit Plane 29
2.5.1 Perifocal Coordinates and the Eccentric Anomaly 29
2.5.2 Kepler's Equation and the Mean Anomaly 32
2.5.3 Newton-Raphson Solution of Kepler's Equation 34
2.5.4 Orbital Position as a Function of Time 35
2.6 Useful Formulas for an Elliptical Orbit 35
2.7 Suggested Reading 37
Chapter 3. Celestial Sphere and ECI Coordinates 39
3.1 Need for an Inertial Reference Frame 39
3.2 The Celestial Sphere 4
3.3 The ECI Reference Frame 42
3.4 Celestial Coordinates and Transformations 43
3.5 Suggested Reading 44
Chapter 4. Rotation Matrices and Applications 45
4.1 Orthogonal Rotation 45
4.2 The EFG-to-ECI Transformation 48
4.3 The Euler Angle Transformation 51
4.4 Suggested Reading 53
Chapter 5. Orbital Elements & Orbit Propagation 55
5.1 Orbital Elements 55
5.2 Velocity in the Orbit Plane 58
5.3 Orbit Propagation 60
5.4 Summary Algorithm for Elliptical Orbit 61
5.5 Modification for an Orbit of Low Eccentricity 63
5.6 Suggested Reading 63
Chapter 6. Dynamical Time Conversion 65
6.1 Sidereal Time 66
6.2 Solar Time 68
6.3 Atomic Time vs. Universal Time 71
6.4 Newcomb's Formula 72
6.5 Suggested Reading 73
Chapter 7. Ground Traces and Look Angles 75
7.1 The Figure of the Earth 76
7.2 Geocentric and Geodetic Latitude 78
7.3 Subpoint Latitude and Height 80
7.4 East Longitude 83
7.5 Look Angles and Slant Range 85
7.6 Suggested Reading 87
Chapter 8. Element Set Transformations 89
8.1 Cartesian-to-Classical Transformation 90
8.1.1 Calculation of a, e, and M 90
8.1.2 Calculation of i, Omega, and omega 92
8.2 Nodal Orbital Elements 94
8.2.1 Transformations Involving Nodal Elements 94
8.2.2 Orbit Propagation Using Nodal Elements 95
8.2.3 Summary Algorithm 100
8.3 Equinoctial Orbital Elements 101
8.3.1 Transformations Involving Equinoctial Elements 102
8.3.2 Orbit Propagation Using Equinoctial Elements 103
8.3.3 Summary Algorithm 109
8.4 Summary 110
8.5 Suggested Reading 112
Chapter 9. Gaussian Orbit Determination 113
9.1 Closed-Form f and g Series 115
9.2 Derivation of Gauss's Method 116
9.2.1 Area Ratio of Sector to Triangle 118
9.2.2 The First Equation of Gauss 119
9.2.3 The Second Equation of Gauss 122
9.2.4 Iteration for E2 - E1 and Solution for a 124
9.3 Summary Algorithm for Gauss's Method 126
9.4 Applications of Gauss's Method 127
9.4.1 Artificial Earth Satellite Orbit Determination 127
9.4.2 Interpolation on Ephemerides 128
9.4.3 Determination of an Avoidance Trajectory 128
9.5 Critique of Gauss's Method 129
9.6 Suggested Reading 130
Chapter 10. Cowell Propagation 133
10.1 Classification of Perturbative Accelerations 136
10.2 Conservative Accelerations 137
10.2.1 Earth's Gravity 137
10.2.2 Sun, Moon, and Major Planet Gravity 140
10.3 Non-Conservative Accelerations 141
10.3.1 Solar Radiation Pressure 141
10.3.2 Atmospheric Drag 144
10.4 Numerical Propagation 145
10.4.1 Reduction of Order 146
10.4.2 Runge-Kutta Numerical Integration 147
10.4.3 Application to the Cowell Problem 148
10.5 Summary 150
10.6 Suggested Reading 150
Chapter 11. Variation of Parameters 153
11.1 Lagrange's Planetary Equations 155
11.1.1 Lagrange's Brackets 157
11.1.2 Lagrange's Brackets for the Classical Elements 158
11.1.3 Substitution of M for M0 164
11.2 Transformation to Other Variables 165
11.3 Gauss's Form of Lagrange's Equations 167
11.4 VOP for Earth's Equatorial Bulge 170
11.5 VOP for Atmospheric Drag 172
11.6 Numerical Integration 175
11.7 Concluding Remarks 176
11.8 Suggested Reading 177
Chapter 12. General Perturbation Theory 179
12.1 Kozai's Method 181
12.2 First-Order, Secular Perturbation Theory 185
12.3 Chebotarev's Method for Small e 187
12.4 Modeling the Drag Acceleration 188
12.4.1 Secular Changes in a and e 188
12.4.2 Two Key Assumptions 191
12.5 Orbit Propagation with Mean Elements 192
12.6 Calculation of Time Elapsed Since Epoch 196
12.7 Concluding Remarks 198
12.8 Suggested Reading 199
Chapter 13. Launch Profiles and Nominals 201
13.1 Calculating Launch Nominal Elements 202
13.1.1 Computation of Omega and M at Injection 203
13.1.2 Computation of a-bar, Given rp or Hp 208
13.1.3 Computation of i and DI from AzI and Converse 209
13.1.4 The Case Where omega is not Specified 210
13.2 Moving Epoch to Revolution Zero 210
13.2.1 Purpose of Moving Epoch 210
13.2.2 Propagation of Mean Elements 211
13.2.3 Computation of n-bar and Delta-tI 212
13.3 The January 1.0 UTC Liftoff Convention 214
13.3.1 When a Cooperative Launch is Delayed 214
13.3.2 Non-Cooperative Launch Assessment 216
13.4 Polar Orbiter Launch Practice 217
13.5 Hypothetical NPOESS Launch Example 219
13.6 Orbital Maneuvers 224
13.6.1 One-Impulse Maneuvers 224
13.6.2 Multiple-Impulse Maneuvers 225
13.6.3 Application of the Hohmann Transfer 228
13.7 Geostationary Launch Practice 228
13.8 Hypothetical GOES Launch Example 231
13.9 Suggested Reading 235
Chapter 14. Escape and Flyby Trajectories 237
14.1 Uniform Path Mechanics 238
14.1.1 Stumpff's c-Functions 239
14.1.2 Conic Elements 249
14.1.3 Uniform Propagation of Conic Elements 250
14.1.4 Kepler's Equation Revisited 260
14.1.5 Propagation of Position and Velocity 263
14.2 Gaussian Orbit Determination 268
14.3 Goodyear's State Transition Matrix 272
14.4 Suggested Reading 275
Chapter 15. Differential Correction 277
15.1 Batch Least Squares 277
15.1.1 Optical Residuals and Partials 282
15.1.2 Radar Residuals and Partials 285
15.1.3 The H Matrix 290
15.1.4 Summary Algorithm 294
15.1.5 HTWH Matrix Accumulation 296
15.2 Variant Orbit Partials 297
15.3 Escape Trajectory Example 299
15.4 State Space Analysis 306
15.4.1 Batch Filter for Two-Body Trajectory 306
15.4.2 Batch Filter for Perturbed Trajectory 308
15.4.3 Batch DC vs. Batch Filter 310
15.4.4 Statistical Orbit Determination 311
15.5 Suggested Reading 312
Appendix A. Astrodynamic Notation 313
A.1 Chapter 1 - Introduction and Review 314
A.2 Chapter 2 - The Two-Body Problem 315
A.3 Chapter 3 - Celestial Sphere and ECI Coordinates 316
A.4 Chapter 4 - Rotation Matrices and Applications 316
A.5 Chapter 5 - Orbital Elements and Orbit Propagation 316
A.6 Chapter 6 - Dynamical Time Conversion 317
A.7 Chapter 7 - Ground Traces and Look Angles 318
A.8 Chapter 8 - Element Set Transformations 319
A.9 Chapter 9 - Gaussian Orbit Determination 319
A.10 Chapter 10 - Cowell Propagation 320
A.11 Chapter 11 - Variation of Parameters 321
A.12 Chapter 12 - General Perturbation Theory 321
A.13 Chapter 13 - Launch Profiles 322
A.14 Chapter 14 - Escape and Flyby 322
A.15 Chapter 15 - Differential Correction 323
A.16 References 323
Appendix B. Astrodynamic Constants 325
B.1 Canonical Units 327
B.2 Precession and Nutation 328
B.3 References 329
Appendix C. Spherical Trigonometry 331
C.1 Spherical Law of Sines 333
C.2 Spherical Law of Cosines for Sides 333
C.3 Spherical Law of Cosines for Angles 334
C.4 Napier's Rules 334
C.5 Earth Satellite Injection 335
C.6 Azimuth Direction from a Point 336
C.7 Radio Wave Propagation 339
C.8 Suggested Reading 339
Appendix D. Chebotarev's Method 341
D.1 Lagrange's Equations for Small e 341
D.2 The Disturbing Potential for Small e 342
D.3 First-Order Perturbations 344
D.3.1 Mean Argument of Latitude 346
D.3.2 Secular and Periodic Updating 348
D.4 Orbit Propagation Procedure 348
D.4.1 Preliminary Calculations 348
D.4.2 Convert to Nodal Elements 349
D.4.3 Update for Secular Perturbations 350
D.4.4 Update for Periodic Perturbations 351
D.4.5 Transform to Position and Velocity 352
D.5 Suggested Reading 352
Index 353
About the Author
Roger L. Mansfield is a space professional with more than 30 years of military, industrial, and academic experience. He began his space career as an orbital analyst for the Defense Meteorological Satellite Program (DMSP) in August 1967, when he wasassigned to the 4000th Support Group at Offutt Air Force Base, Nebraska. (Offutt AFB is now the home of Headquarters U.S. Strategic Command.)
As principal engineerfor space surveillance applications at Ford Aerospace and at Loral Command & Control Systems, Mr. Mansfield led efforts to develop algorithms and software for the 427M Space Surveillance Center (1976-1981) and for the Space Defense Operations Center (1982-1996) in Air Force Space Command's Cheyenne Mountain Air Force Station. As assistant professor at CU-Colorado Springs, hetaught astrodynamics and numerical methods to graduate space engineers working for Lockheed Martin Astronautics at the Waterton Canyon facility near Denver, Colorado.
Mr. Mansfield's personal webpage athttp://mathcadwork.astroger.com/ describes just a few of the Mathcad worksheets he has constructed since 1997 to solve problems in the mechanics of Earth orbital, escape, flyby, and interplanetary trajectories. His freely downloadable Mathcad worksheets provide live,graphical examples of many of the algorithms and procedures in his book. And the worksheets employ familiar mathematical notation, not ASCII program code.
With 'Nicolaus Copernicus' at AGI's 15th Annual Monte Carlo Night, April 2015
How to Purchase the Book
The book's intended audience has been: military and civilian members of the U.S. Air Force; other U.S. governmental departments and agencies dealing with space; the U.S. space industry; professors and students of space engineering.
Return to the Lessons Index | Do the Lessons in Order | Print-friendly page |
Conic Sections: An Overview
Conic sections are the curves which can be derived from taking slices of a 'double-napped' cone. (A double-napped cone, in regular English, is two cones 'nose to nose', with the one cone balanced perfectly on the other.) 'Section' here is used in a sense similar to that in medicine or science, where a sample (from a biopsy, for instance) is frozen or suffused with a hardening resin, and then extremely thin slices ('sections') are shaved off for viewing under a microscope. If you think of the double-napped cones as being hollow, the curves we refer to as conic sections are what results when you section the cones at various angles.Copyright © Elizabeth Stapel 2010-2011 All Rights Reserved
Advertisement
There are plenty of sites and books with pictures illustrating how to obtain the various curves through sectioning, so I won't bore you with more pictures here. And there are books and entire web sites devoted to the history of conics, the derivation and proofs of their formulas, and their various applications. I will not attempt to reproduce that information here.
This lesson, and the conic-specific lessons to which this page links, will instead concentrate on: finding curves, given points and other details; finding points and other details, given curves; and setting up and solving conics equations to solve typical word problems.
There are some basic terms that you should know for this topic:

- center: the point (h, k) at the center of a circle, an ellipse, or an hyperbola.
- vertex (VUR-teks): in the case of a parabola, the point (h, k) at the 'end' of a parabola; in the case of an ellipse, an end of the major axis; in the case of an hyperbola, the turning point of a branch of an hyperbola; the plural form is 'vertices' (VUR-tuh-seez).
- focus (FOH-kuss): a point from which distances are measured in forming a conic; a point at which these distance-lines converge, or 'focus'; the plural form is 'foci' (FOH-siy).
- directrix (dih-RECK-triks): a line from which distances are measured in forming a conic; the plural form is 'directrices' (dih-RECK-trih-seez).
Basic Astrodynamics Formulas For Beginners
- axis (AK-siss): a line perpendicular to the directrix passing through the vertex of a parabola; also called the 'axis of symmetry'; the plural form is 'axes' (ACK-seez).
- major axis: a line segment perpendicular to the directrix of an ellipse and passing through the foci; the line segment terminates on the ellipse at either end; also called the 'principal axis of symmetry'; the half of the major axis between the center and the vertex is the semi-major axis.
- minor axis: a line segment perpendicular to and bisecting the major axis of an ellipse; the segment terminates on the ellipse at either end; the half of the minor axis between the center and the ellipse is the semi-minor axis.
- locus (LOH-kuss): a set of points satisfying some condition or set of conditions; each of the conics is a locus of points that obeys some sort of rule or rules; the plural form is 'loci' (LOH-siy).
You may encounter additional terms, depending on your textbook. Just make sure that you understand the particular terms that come up in your homework, so you're prepared for the test.
One very basic question that comes up pretty frequently is 'Given an equation, how do I know which sort of conic it is?' Just as each conic has a typical shape:
...so also each conic has a 'typical' equation form, sometimes along the lines of the following:
parabola: Ax2 + Dx + Ey = 0
circle: x2 + y2 + Dx + Ey + F = 0
ellipse: Ax2 + Cy2 + Dx + Ey + F = 0
hyperbola: Ax2 – Cy2 + Dx + Ey + F = 0
These equations can be rearranged in various ways, and each conic has its own special form that you'll need to learn to recognize, but some characteristics of the equations above remain unchanged for each type of conic. If you keep these consistent characteristics in mind, then you can run through a quick check-list to determine what sort of conic is represented by a given quadratic equation.
Given a general-form conic equation in the form Ax2 + Cy2 + Dx + Ey + F = 0, or after rearranging to put the equation in this form (that is, after moving all the terms to one side of the 'equals' sign), this is the sequence of tests you should keep in mind:
- Are both variables squared?
- Do the squared terms have opposite signs?
- Are the squared terms multiplied by the same number?
No: It's a parabola.
Yes: Go to the next test....
Yes: It's an hyperbola.
No: Go to the next test....
Yes: It's a circle.
No: It's an ellipse.
- Classify the following equations according to the type of conic each represents:
A) 3x2 + 3y2 – 6x + 9y – 14 = 0
B) 6x2 + 12x – y + 15 = 0
C) x2 + 2y2 + 4x + 2y – 27 = 0
D) x2 – y2 + 3x – 2y – 43 = 0
A) Both variables are squared, and both squared terms are multiplied by the same number, so this is a circle.
B) Only one of the variables is squared, so this is a parabola.
C) Both variables are squared and have the same sign, but they aren't multiplied by the same number, so this is an ellipse.
D) Both variables are squared, and the squared terms have opposite signs, so this is an hyperbola.
If they give you an equation with variables on either side of the 'equals' sign, rearrange the terms (on paper or in your head) to get the squared stuff together on one side. Then compare with the flow-chart above to find the type of equation you're looking at.
You may have noticed, in the table of 'typical' shapes (above), that the graphs either paralleled the x-axis or the y-axis, and you may have wondered whether conics can ever be 'slanted', such as:
Yes, conic graphs can be 'slanty', as shown above. But the equations for the 'slanty' conics get so much more messy that you can't deal with them until after trigonometry. If you wondered why the coefficients in the 'general conic' equations, such as Ax2 + Cy2 + Dx + Ey + F = 0, skipped the letter B, it's because the B is the coefficient of the 'xy' term that you can't handle until after you have some trigonometry under your belt. You'll probably never have to deal with the 'slanty' conics until calculus, when you may have to do 'rotation of axes'. Don't be in a rush. It's not a pretty topic.
Once you have classified a conic, what can you do with it? The following lessons give some examples:
Parabolas | Circles | Ellipses | Hyperbolas
Basic Astrodynamics Formulas Chart
Top | Return to Index
Basic Astrodynamics Formulas Free
Cite this article as: | Stapel, Elizabeth. 'Title Goes Here.' Purplemath. Available from |
